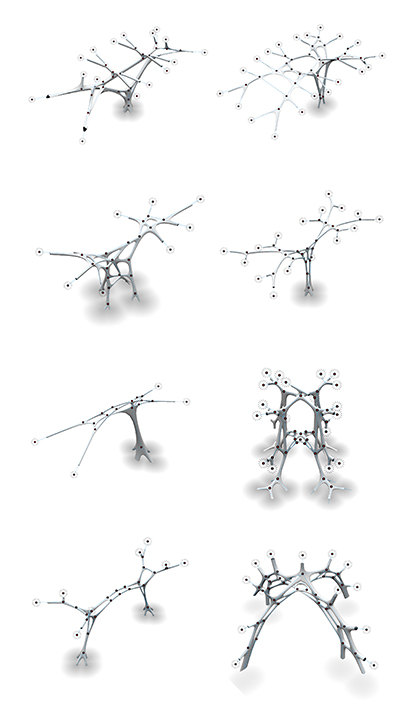






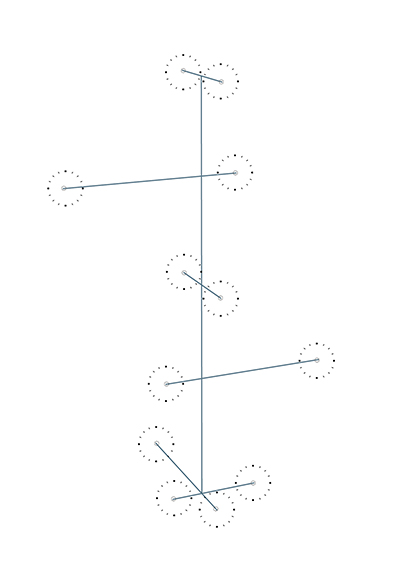
















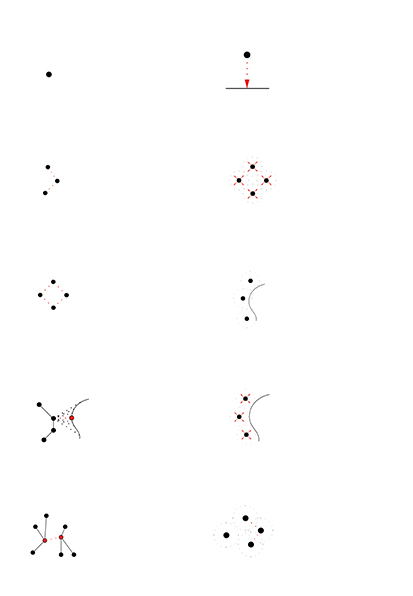
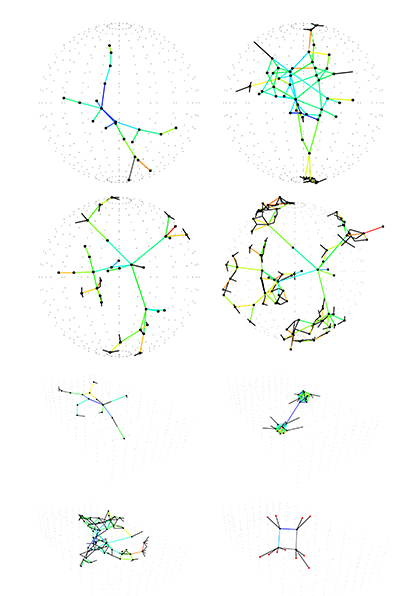


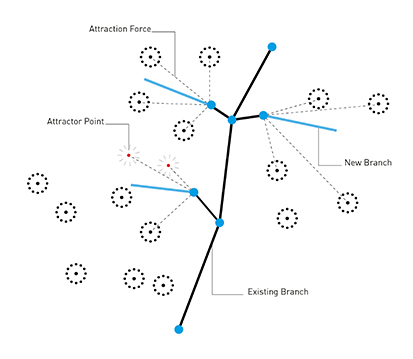



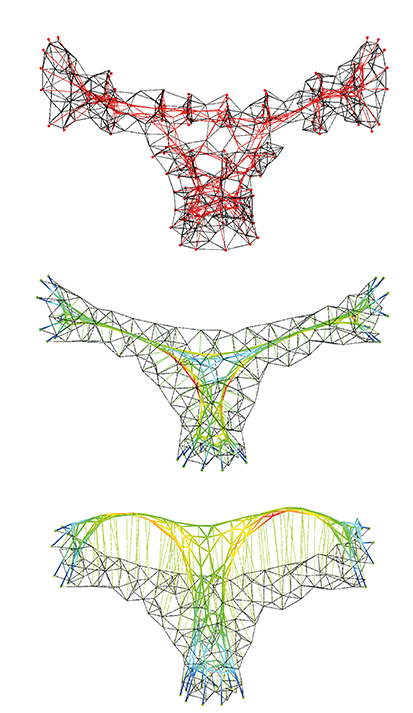
Fixed Nodes
Free Nodes
Compression Members
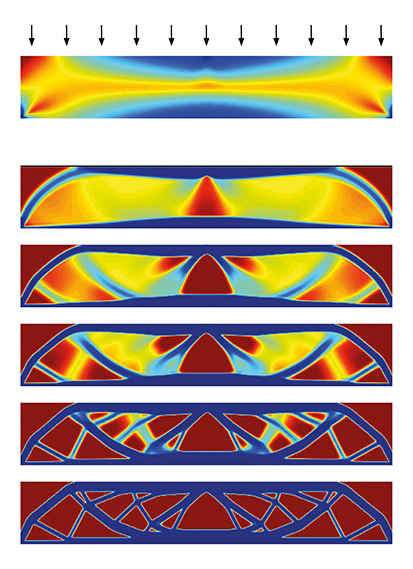
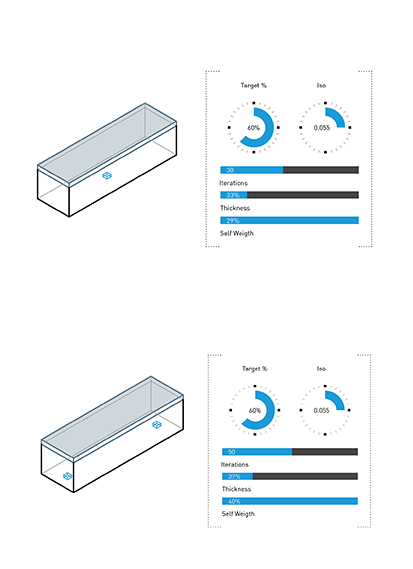
Compression only graph with minimal deviation from the given graph according to the given loads and self weight.
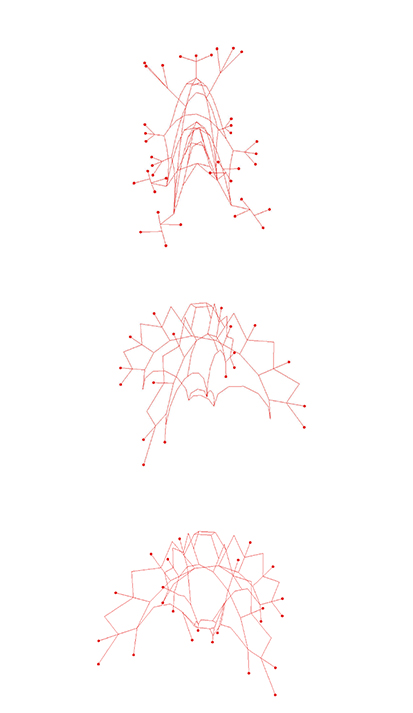
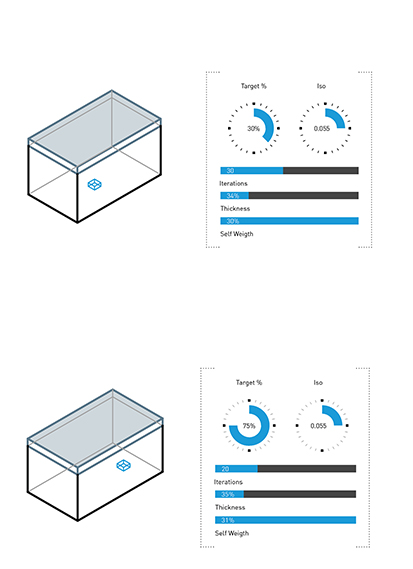
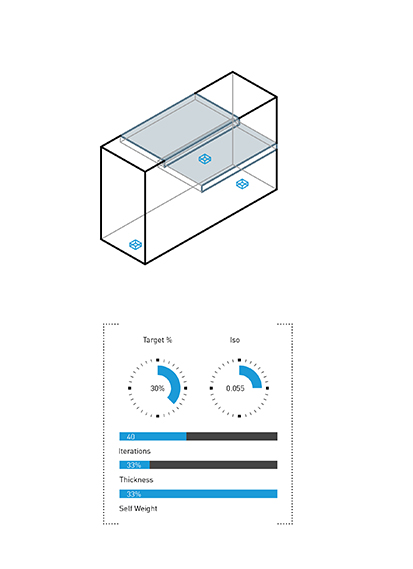
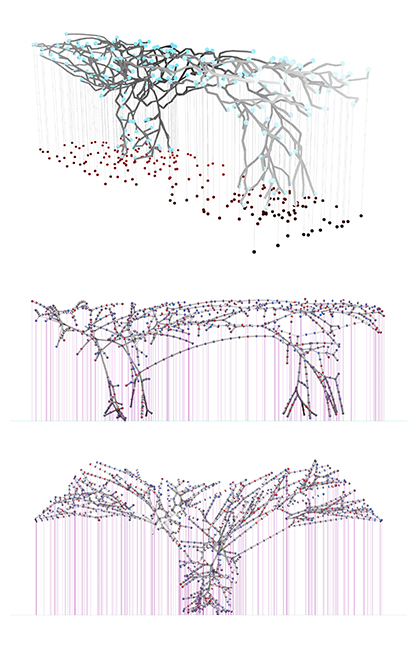
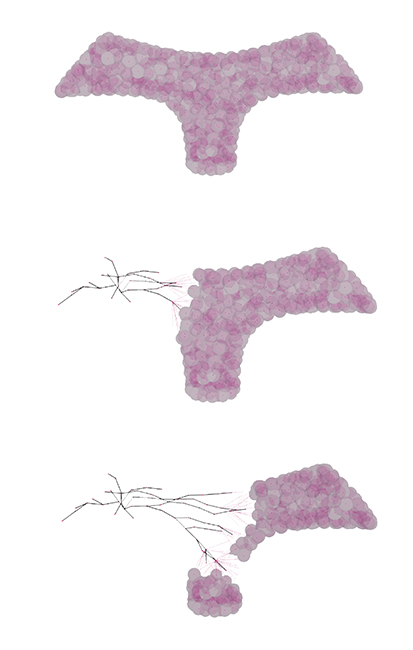
Manually modeled geometric inputs.
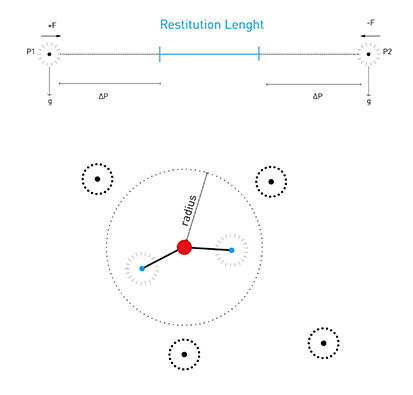
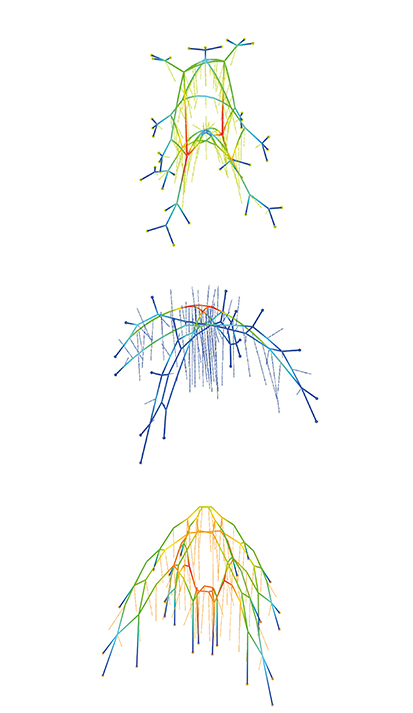
Resultant compression-only graph where the force density in each member is the same i.e the ratio of force to length in each member is the same.
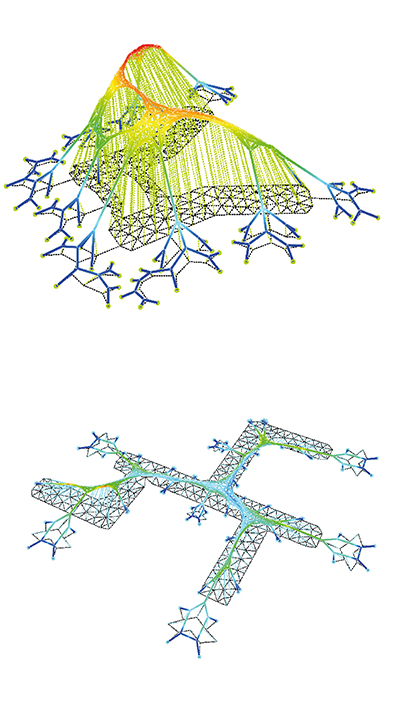
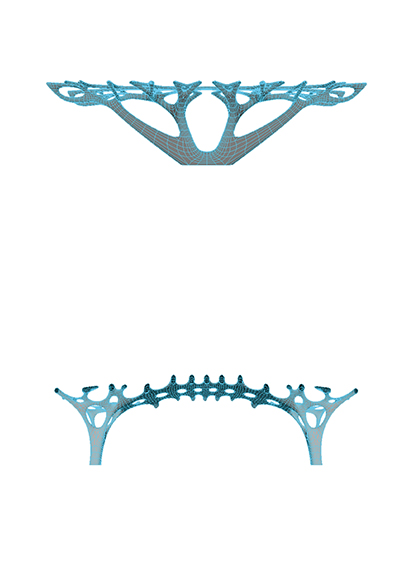
Compression only graphs computed through dynamic relaxation method.
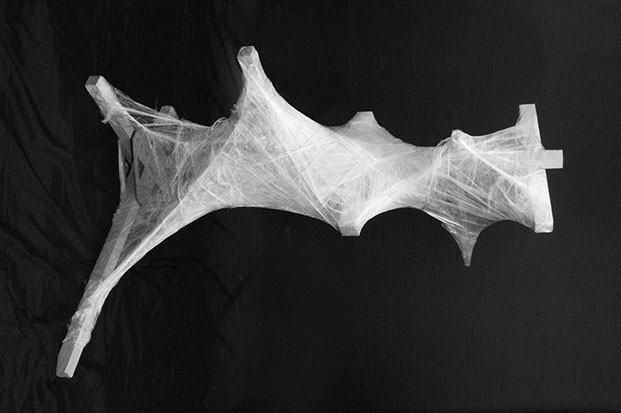
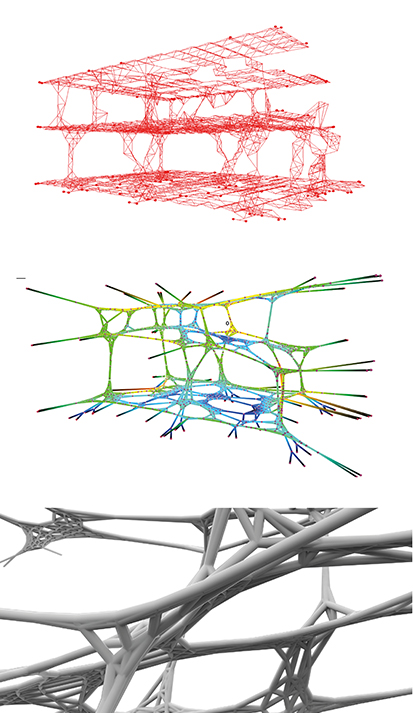
Outline of the Domino House skeletal geometry used as an input to same algortihm.